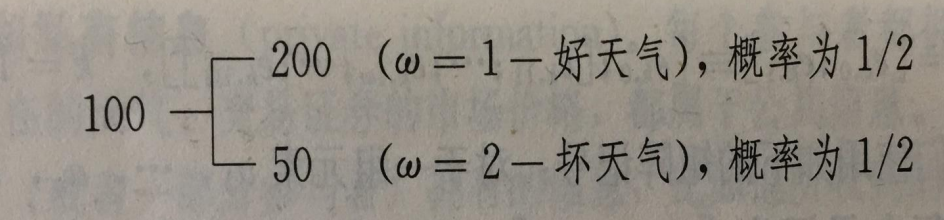-
第二章
-
基本的理论框架
-
经济学经济结构
- 他所处自然环境
- 时间、风险
- 经济中各参与者(agent)的经济特征
- 金融市场
- 他所处自然环境
-
描述经济环境
- Lucas 树
- 经济状态可以用 Lucas 树来描述。
- Lucas 树经济
- Lucas 树
- 描述经济参与者的经济资源
- 禀赋(endowment)
- 概念:参与者初始占有的资源是他与生俱来的商品和/或资本品,可以用作消费或生产。
- 可以表示为一个每一时期和(未来)每一状态下拥有的商品
- \(e_{k}\equiv[e_{k,0},e_{k,1}]=[e_{k,0};[e_{k,11};\cdots;e_{k,1\omega};\cdots e_{k,1\Omega}]]\)
- 信息
- 公共信息
- 私有信息
- 生产技术
- 简化假设不考虑
- 禀赋(endowment)
-
参与者的经济需求
- 经济需求基于消费描述
- 消费集
- 偏好
- 对所有可能消费计划中的一个排序。排序定义了经济需求
- 偏好的假设
- 完备性(任意两个消费可比较)
- 传递性
- 偏好的基本假设
- 不满足性
- 连续性
- 凸性
- \(\forall a,b\in C,a\in(0,1)\), if \(a>_{p}b\), then \(\alpha a+(1-\alpha)b>+p>b\)
- 效用函数
- 对每一个消费计划赋予一个实数(效用)。符合偏好假设的从消费计划到实数的映射
-
证券市场建模
- 市场结构?\(X\)
- 二维矩阵。payoff matrix
- 横轴 n 个股票,每一列向量是一个股票在 \(\Omega\) 状态集合中各状态的支付
-
证券组合?\(\theta\)
- \(\theta\equiv[\theta_{1};\dots;\theta_{n};\dots;\theta_{N}]\)
-
市场化
- 一个支付 \(x\) 可以由市场产生,就说可以市场化(marketed)
- \(M\equiv \{ X\theta: \theta \in R^{N} \}\)
- 价格向量
- \(S\equiv[S_{1};\dots;S_{n};\dots;S_{N}]\)
- 基本经济模型
- 状态
- 参与者
- 信息
- 禀赋
- 偏好
- \(X\) 的无摩擦证券市场
- 市场出清
- 总需求等于总供给
- 需求:消费
- 供给:禀赋
- 推导出 \(\sum_{k}c_{k}=\sum_{k}e_{k}\)
- \(\sum_{k}\theta_{k}(e_{k},S)=0\)
- 总消费等于总禀赋
- 总需求等于总供给
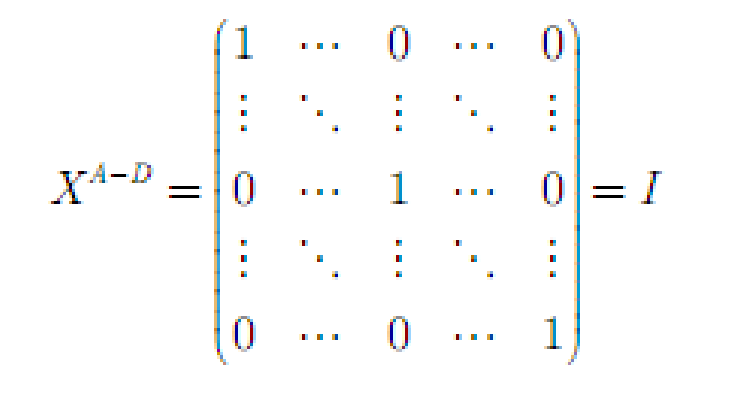
- Arrow-Debreu 证券市场
- 或有要求权(state-contingent security)
- 依情况而定的证券
- 状态是 0 或 1 的,即 iff \(\omega'=\omega\) 时有一个单位的支付
- 市场结构为单位矩阵(如果恰当的排列状态)
- 状态价格
- \(\phi_{\omega}\) : state \(\omega\) 或有证券在 0 期的价格(以 0 期的消费品为单位)
- 状态价格必须为正
- 如果为负,则参与者可以得到证券并得到眼下的收入。free lunch
- 参与者禀赋的市场价值为 \(w=e_{0}+\phi^{T}e_{1}\)
- 是一种未来禀赋的贴现
- 预算约束:
- \(c_{0}+\phi^{T}c_{1}=w=e_{0}+\phi^{T}e_{1}\)
- 方便记录,将 1 单位 0 期消费品的价格 \(\phi_{0}\) 当作第一个元素,而 \(\phi_{0}=1\)
预算约束:
- 优化问题

- 上述优化问题的 Lagrangian 函数
- 注:关于 Lagrangian 函数可以阅读 lagrangian 函数和优化问题
- 总体来说,就是将约束条件加权。这里选择的权重为 \(\lambda\) 和很多个 \(\mu_{i}\)(每个对应一个 \(c\))
- \(\frac{{\partial L}}{\partial c_{i}}=0\)
- \(\frac{{\partial L_{i}}}{\partial\lambda}=0\)
- \(\frac{{\partial L}}{\partial \mu_{i}}=0\)
- 以上是一阶条件
解释上面的优化条件式子
- \(\lambda,\mu\) 是广义 Lagrangian 乘子
- 最优解受到约束制约,对应的乘子为正。否则为 0
- \(\mu_{i}\) 有非负要求。
 - 求出最优消费选择后,怎么求均衡状态价格?
- 利用市场出清条件,解方程
- 求出最优消费选择后,怎么求均衡状态价格?
- 利用市场出清条件,解方程
- 第 4 章 - 套利和资产定价
- 冗余证券概念
- 去掉它,仍然可以表达市场。
- 它的支付是其他证券支付的线性组合
- 证券市场的等价描述
- 用独立的组合 \([\theta]\) 来等价描述市场结果
- 满秩变换
- Span
- 满秩(span=n)的市场结构,可以由 A-D 经济生成。(0-1 矩阵)
-
必考 套利¶
- 即吃到了免费的午餐
- 没有付出得到了回报。
- 第 I 类套利 - 无成本
- \(S^{T}\theta<0,X\theta=0\)
- 用二进制容易记忆套利 123... =是 0,否则为 1
01,1(先看 X,再看 S)
- 第 II 类套利 无风险
- \(S^{T}\theta=0,X\theta>0\)
- 初始投资为 0 的组合,为套利组合
10,2
- 第 III 类套利 有收益
- \(S^{T}\theta<0,X\theta>0\)
11,3
- 定理:市场均衡中不存在套利机会(无套利原理)

- 资产定价基本定理
- Law of One Price (LOP) 一价定律
- 相同支付的证券价格必定相同
- 支付为正的证券的价格为正
- 如果支付总是高,则价格必定高
- 定价算子是递增的线性算子(如果无摩擦市场)
- 完全的证券市场中,价格状态向量 \(\phi\) 唯一
-
举个例子来说明定价操作

- 可以得见,定价过程就是对于对于每个证券分别得到其状态价格向量的空间,然后取 交集
- 可见 A、B、C 找不到无套利定价,这就说明 A、B、C 组成的证券可以套利。
-
风险中性定价
- 假设市场存在一支无风险债券,1 期的支付确定,令其为 \(x_{1}=[1;1;\dots;1]=\iota\)
- 利率
- 无风险利率
- \(S_{1}(1+r_{F})=1\), or \(r_{F}=\frac{{1-S_{1}}}{S_{1}}\)
- 数学变换:\(\frac{1}{r_{F}+1}=S_{1}=\sum_{\omega}\phi_{\omega}\)
- So, 债券定价可以由利率
- \(S_{1}=\frac{1}{1+r_{F}}=\sum_{\omega}\phi_{\omega}\)
- \(\dfrac{1}{1+r_{F}}\):贴现因子,\(r_{F}\):折现率
- 其他证券的定价
- 比如支付为 \(\tilde{X}=X_{\cdot,n}=[x_{1,n};\cdots;x_{\Omega,n}]\) 的证券 \(n\)
- 定价为 \(S_{n}=\phi^{T}\tilde{X}_{n}=\sum_{\omega}\phi_{\omega}x_{\omega,n}\)
- 换个测度, 试图用无风险债券 \(S_{1}\) 换元
- \(q_{\omega}=\frac{\phi_{\omega}}{\sum_{\omega}\phi_{\omega}}\). \(Q\equiv \{ q_{\omega},\omega \in \Omega \}\)(\(Q\) 称为 risk-neutral measure)
- \(S_{n}=\frac{1}{1+r_{F}}E^{Q}[\tilde{X}_{n}]\)
- 注意,\(\tilde{X}_{1}=1\), 所以资产定价公式也可以写作
$$ \frac{S_{n}}{S_{1}}=E^{Q}\left[ \frac{\tilde{X}{n}}{\tilde{X}{1}} \right] $$ - 如果使用 1 单位的证券 1 作为价格计算单位,就回得到 - \(\tilde{S}_{n,t}=E^{Q}[\tilde{S}_{n,t+1}]\)
-
鞅
- 如果一个随机过程,\(z_{1},z_{2},\dots\) 现在的值恒等于其对于其未来值的条件期望,即 \(z_{t}=E_{t}[z_{t+1}]\) ,我们称之为鞅。
- 以无风险债券价格作为计量单位,证券价格在风险中性测度 \(Q\) 下是鞅
-
期望效用函数
- 独立性公理
- 假设消费计划 \(c\) 与 \(c'\) 相对于某一状态有相同的消费路径 \(x\) 并且 \(c\succeq c'\),那么,如果把 \(x\) 换成另一个消费路径 \(y\),\(c\) 和 \(c'\) 的排序不变
- 不同状态下消费(不同消费路径)得到的费用之间彼此独立
- 效用函数形式
- State independence
- 效用和状态无关 \(u_{\omega}(c_{0},c_{1\omega})=u(c_{0},c_{1\omega})\)
- \(U(c)=\sum_{\omega}p_{\omega}u(c_{0},c_{1\omega})\)
- 时间可加性:
- 一个路径得到的效用是各期消费之和
- \(U(c)=u_{0}(c_{0})+\sum_{\omega}p_{\omega}u_{1}(c_{1\omega})\)
- 一阶风险厌恶(期望)
- 伯努利:最大期望效用解决彼得堡大街悖论
- 二阶风险厌恶(方差)
- 风险厌恶 (Risk Aversion)
- 边际效用递减
- 风险溢价:参与者为了消除风险而愿意放弃的财富值
- 小风险赌博:
- \(E[\tilde{g}^{2}]=var[\tilde{g}]+(E[\tilde{g}])^{2}=var[\tilde{g}]\)
- 小风险:方差是风险大小的度量
- 绝对风险厌恶
-
Arrow-Pratt measure of risk aversion
-
\(A(w)=-{\frac{u''(w)}{u'(w)}\geq} 0\)
-
风险容忍系数 risk tolerance coefficient \(T(w)\equiv {\frac{1}{A(w)}=-{\frac{u'(w)}{u''(w)}}}\)
- 相对风险厌恶
- 考虑了风险对于参与者的总财富的相对大小
- \(E[u(w(1+\tilde{g}))]=u(w(1-\pi_{R}))\)
- 盈亏和财富称遍历,相对的风险溢价也为如此
- \(\pi_{R}=\frac{1}{2}\left[ -{\frac{wu''(w)}{u'(w)}} \right]var[\tilde{g}]\)
- 相对风险厌恶 \(R(w)\)
- \(R(w)\equiv-\frac{{wu''(w)}}{u'(w)}\)
- 需要会根据式子计算风险溢价
-
-
风险厌恶的比较
- 越凹风险越厌恶
- 下面命题等价
- \(A_{1}(w)\geq A_{2}(w),\forall w\)
- \(u_{1}(u_{2}^{-1}(z))\), concave
- \(\exists f(\cdot)\) with \(f'(\cdot)>0\) and \(f''(\cdot)\leq 0\) s.t. \(u_{1}(w)=f[u_{2}(w)]\)
- \(u_{1}(w)=f[u_{2}(w)]\),1 的效用函数更凹,也就是 1 的效用函数是 2 的效用函数的一个凹变换
- \(\pi_{1}\geq \pi_{2},\forall w\text{ and gambles}\)(赌博)
- 组合选择
- 优化问题两种表述
- (8.1)
- \(\max_{\theta} u_{0}(c_{0})+\sum_{\omega \in \Omega}\pi_{\omega}u_{1}(c_{1\omega})\)
- s.t.
- \(c_{0}=e_{0}-S^{T}\theta\)
- \(c_{1}=e_{1}+X\theta\) (预算约束,1 期总消费等于 1 期总财富(禀赋+市场回报))
- \(c_{0},c_{1}\geq 0\)
- (2.6)
- \(\max_{\theta_{k}}u_{k}(c_{k})\)
- s.t.
- \(c_{k,0}=e_{k,0}-S^{T}\theta_{k}\)
- \(c_{k,1}=e_{k,1}+X\theta_{k}\)
- \(c_{0},c_{1}\geq 0\)
- 解的存在性
- 上式有解 iff \(\{ X,S \}\) 不存在套利机会
- 将 8.1 式子带入预算约束 \(e_{1\omega}+X_{\omega,\cdot}\theta=c_{1\omega}\)
- 一阶条件
- \(u_{0}'(c_{0})S_{n}=\sum_{\omega \in \Omega}p_{\omega}u_{1}'(c_{1\omega})x_{\omega,n}=E[u_{1}'(\tilde{c}_{1})\tilde{X}_{n}],n=1,\dots,N\)
- 即 Euler 方程
- 也可以表述为 \(E\left[ \dfrac{u_{1}'(\tilde{c}_{1}\tilde{X}_{n} )}{u_{0}'(c_{0})S_{n}} \right]=1\)
- 含义:参与者在今天消费最后一元,和把它用来投资和取得明天的消费之间是无差异的
- 投资对于今天消费的相对标记效用全部等于 1
- 对于凹的期望函数,一阶条件是充分条件。
- 我们考虑简化的组合选择问题
- \(v(w)=\max_{(\theta,S^{T}\theta=w}E[u(\tilde{X}\theta)]\)
- 总收益率 \(\tilde{x}_{n}=\frac{\tilde{X}_{n}}{S_{n}}\)
- net rate of return \(\tilde{r}_{n}\equiv \frac{{\tilde{X}_{n}-S_{n}}}{S_{n}}\)
- 引入无风险债券,利率为 \(r_F\),则可以进一步简化
- \(\tilde{w}=\sum_{n}\theta_{n}\tilde{X}_{n}=\sum_{n}a_{n}\tilde{x}_{n}=\sum_{n}a_{n}(1+\tilde{r}_{n})\)
- \(\tilde{w}=w(1+r_{F})+\sum_{n=1}^{N}a_{n}(\tilde{r}_{n}-r_{F})\)
- 其中 \(w=\sum_{n}a_{n}\)
- 超额收益率 excess return \(\tilde{r}_{n}-r_{F}\)
- 经过简化,得到
- \(\max_{a}E[u(\tilde{w})]=E\left[ u(w(1+r_{F}))+\sum_{n=1}^{N-1}a_{n}(\tilde{r}_{n}-r_{F}) \right]=E[u(w(1+r_{F})+a^{T}(\tilde{r}-r_{F}\iota))]\)
- 求解上面式子的一阶条件
- \(E[u'(\tilde{w})(\tilde{r}_{n}-r_{F})]=0,n=1,\dots,N-1\)
- 其中 \(\tilde{w}=w(1+r_{F})+a_{n}(\tilde{r}_{n}-r_{F})\)
- 给出了求解 \(a\) 的 N-1个等式
- \(E[u'(\tilde{w})(\tilde{r}_{n}-r_{F})]=0,n=1,\dots,N-1\)
-
最优组合的期望收益率大于无风险收益率
-
随机占优
- 考虑收益率:
- 期望收益率
- 风险
- FSD(First Order Stochastic Dominance)
- \(A\) dominates \(B\) in the sense of FSD if \(\forall u'(\cdot)\geq 0\), s.t. \(E[u(\tilde{x}_{A})]\geq E{(u(\tilde{x}_{B}))}\)
- A一阶占优于 B,则 A 和无风险债券的组合占优于 B 和无风险债券的组合
- SSD (Second Stochastic Dominance)
- \(A\) dominates \(B\) in the sense of SSD, denotes as \(A\succeq_{SSD} B\), if \(\forall u''(\cdot)\leq {0}\), \(E[u(\tilde{x}_{A})]\geq E[u(\tilde{x}_{B})]\)
- 其对效用函数的 \(u'(\cdot)\) 没有要求
- 所以我们可以取负来得到期望收益相等的情况,然后就只和风险有关了。
- 这个意义上,二阶随机占优在收益率相等的基础上,比较了两只证券或组合的风险
- 等价表述
- \(A\succeq_{SSD}B\)
- \(E[\tilde{x}_{A}]=E[\tilde{x}_{B}]\), and \(\int_{0}^{y}[F_{A}(x)-F_{B}(x)]dx\equiv S(y)\leq 0,\forall y\)
- 表达的实际是期望相同,但是 \(A\) 获得相同大值的概率更低,即 \(A\) 有更大的机会获得更高的值。
- \(\tilde{x}_{B}\sim_{d}\tilde{x}_{A}+\tilde{e}\), and \(E[\tilde{e}|\tilde{x}_{A}]=0\)
- 这个是比较本质的表述。同分布,两边同取期望是一样的,但是由于 \(\tilde{x}_{A}+\tilde{e}\) 引入了又一个独立的随机变量,所以 \(\tilde{x}_{B}\) 的方差更大。
- 组合分离

-
(即股票不全线性无关),所以可以找到最小的线性无关的股票空间,作为基金组合。
- 对投资方案进行化简(股票组合->基金)
- 每一个参与者的最优组合都是F只基金的线性组合。参与者只需要考虑F支基金的组合,这F支基金就叫做分离基金,这种情形叫共同基金分离
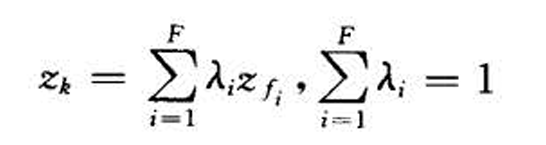
-
分离基金的集合不是唯一的,给定一个分离基金的集合,这些基金的线性组合也可以作为分离基金。
- 基表示不唯一
-
无风险证券作为分离基金之一时的情况也称为货币分离

-
两基金分离


- &&

- &&


- 单基金分离
- &&


- 理解
- 可以用单基金表示。
- 均值 - 方差偏好 (mean-variance preference)
- 假设期望效用 \(E[u(\tilde{w})]\) 取决于期望和方差(是期望方差的函数)
- \(E[u(\tilde{w})]=v(E[\tilde{w}],\sigma[\tilde{w}])\)
- 均值方差偏好
-
知道如何证明均值方差偏好
- \(E\left[ \tilde{w}-\frac{1}{2}a\tilde{w}^{2} \right]=E[\tilde{w}]-\frac{1}{2}aE[\tilde{w}^{2}]=E[\tilde{w}]-\frac{1}{2}a[E[\tilde{w}]^{2}+Var[\tilde{w}]]\)
- \(E[u(\tilde{w})]=v(\tilde{w},\sigma_{w})\)
-
常见的均值方差偏好的分布
- 正态分布的偏好
- 二次型偏好
-
均值方差前沿组合(MVF)
- 一些定义
- \(\Sigma\) 能干什么
- 计算总方差
- \(\sigma_{z}^{2}=Var\left[ \sum_{i=1}^{N}z_{i}\tilde{r}_{i} \right]=z^{T}\Sigma z\)
- 计算两个组合的收益率协方差
- \(\tilde{r}=[\tilde{r}_{1};\tilde{r}_{2};\cdots;\tilde{r}_{N}]\)
- \(\tilde{r}_{p}=z_{p}^{T}\tilde{r}\)
- \(\tilde{r}_{q}=z_{q}^{T}\tilde{r}\)
- \(Cov[\tilde{r}_{p},\tilde{r}_{q}]=Cov[z_{p}^{T}\tilde{r},z_{q}^{T}\tilde{r}]\)
- 计算总方差
- MVF 优化问题
- \(\min \frac{1}{2}z^{T}\Sigma z\)
- \(s.t.\; z^{T}\bar{r}=\bar{r}_{p}\)
- \(z^{T}\iota=1\)
-
给出均值方差前沿组合 (MVF, mean-variance frontier portfolio)
- \(\Sigma\) 是严格正定的,因为假设 \(N\) 只证券都是风险债券,且收益率不线性相关。(也就是方差和协方差都>0)
-
任何一个有均值方差偏好的参与者的最优组合是一个 均值-方差前沿组合
- 含有约束条件的拉格朗日方程
- \(L=\frac{1}{2}z^{T}\Sigma z+\lambda_{r}(\bar{r}_{p}-z^{T}r)+\lambda_{l}(1-z^{T}\iota)\)
- 一阶条件
- \(\frac{{\partial L}}{\partial z}=\Sigma z-\lambda_{r}\bar{r}-\lambda_{l}\iota=0\) (\(n\) 个方程)
- \(\frac{{\partial L}}{\partial \lambda_{r}}=\bar{r}_{p}-z^{T}\bar{r}=0\)
- \(\frac{{\partial L}}{\partial\lambda_{1}}=1-z^{T}\iota=0\)
-
\(\Sigma\) 正定保证二阶条件自然满足
-
可以解出。对于每一个 \(\bar{r}_{p}\) 存在唯一的前沿组合。取不同的 \(\bar{r}_{p}\) 得到完全集合,就叫 MVF
- MVF 曲线(\(\bar{r}-\sigma\) 平面)
-
必考¶
- \(\sigma_{p}^{2}=\frac{c}{d}\left( \bar{r}_{p}-\frac{a}{c} \right)^{2}+\frac{1}{c}\)
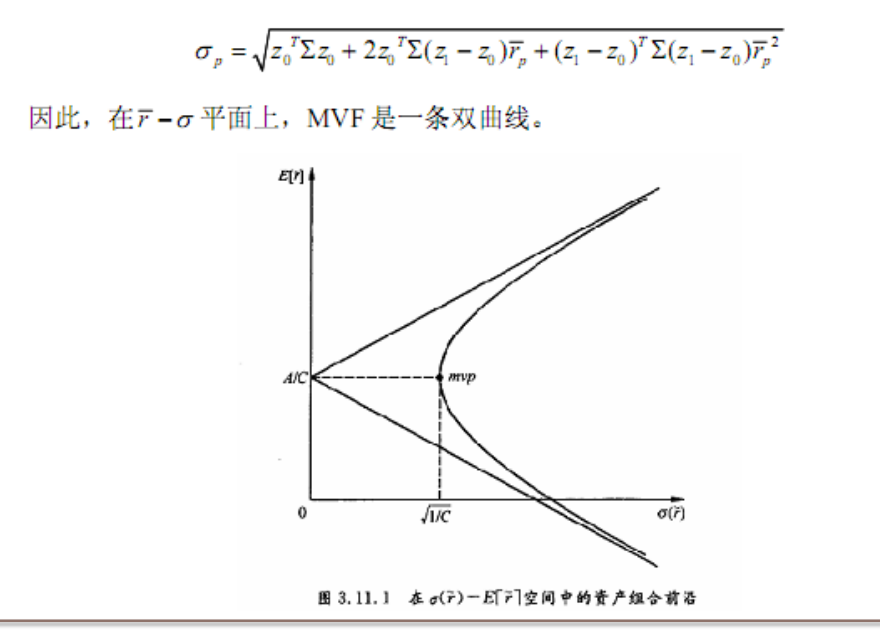
- MVE 是双曲线的上半部分
-
MVE(均值方差有效组合)
- 双曲线的上半部分。
- MVP(minimum variance portfolio, MVP)
- \(\frac{1}{2}\partial \sigma_{p}^{2}/\partial \bar{r}_{p}=0\)
- \(MVP\) 的收益率是 \(\dfrac{a}{c}\)

- \(zcp\) 组合

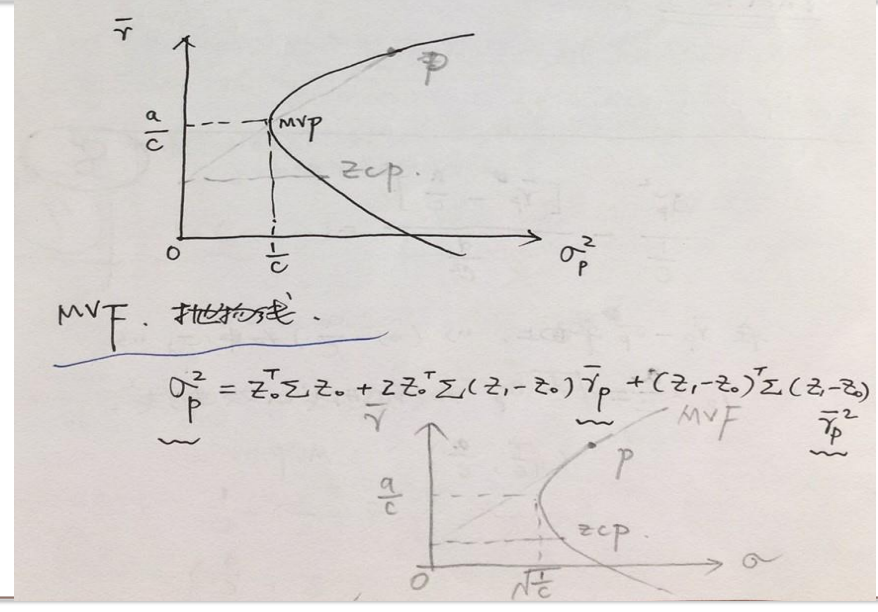
- 对于任意组合 \(p\),\(Cov[\tilde{r}_{p},\tilde{r}_{mvp}]=\sigma_{mvp}^{2}\)
-
\(zcp\):(zero-covariance portfolio)
- 对于任意 MVF 组合 \(p\)(\(\neq MVP\)),存在一个 \(MVE\) 组合 \(zcp\) 使得 \(Cov(\tilde{r}_{p},\tilde{r}_{zcp})=0\)
-
存在无风险资产的情形
- MVF 定义
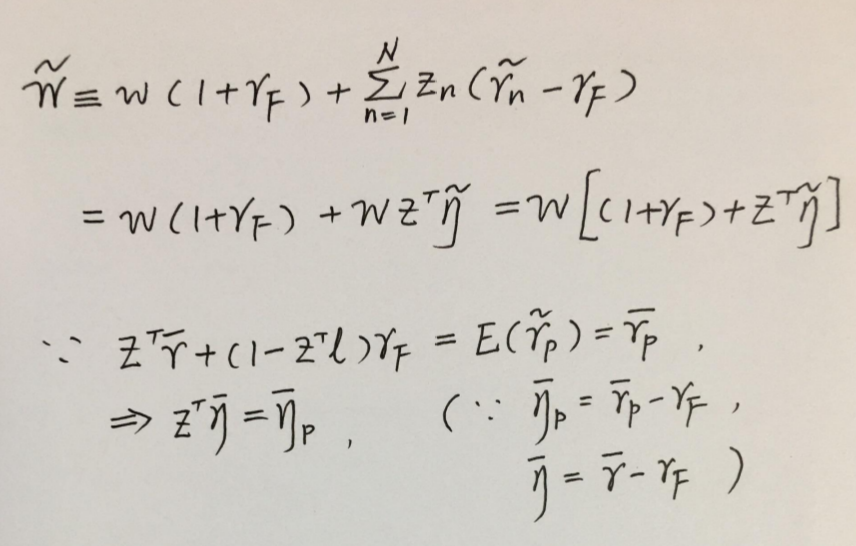
- 现在引入了 \(\bar{\eta}_{p}\) 作为在 \(p\) 上的期望超额收益(expected excess return on \(p\))
- \(\eta\) 是超额收益(相对无风险)的向量, \(\bar{\eta}=\bar{r}-r_{F}\)
- \(z_{p}=\text{Argmin}\; {\frac{1}{2}z^{T}\Sigma z}\)
- s.t \(z^{T}\bar{\eta}=\bar{\eta}_{p}\)
- 拉格朗日方程
- \(L=\frac{1}{2}z^{T}\Sigma z-\lambda[\bar{\eta}_{p}-z^{T}\bar{\eta}]\)
- f.o.c
- \(\frac{{\partial L}}{\partial z}=\Sigma z-\lambda \bar{\eta}=0\)
- \(\frac{{\partial L}}{\partial\lambda}=\bar{\eta}_{p}-z^{T}\bar{\eta}=0\)
- \(z_{p}=\dfrac{\bar{\eta}_{p}}{\bar{\eta}^{T}\Sigma^{-1}\bar{\eta}}\Sigma^{-1}\bar{\eta}\)
- where we assume \(\bar{\eta}^{T}\Sigma^{-1}\bar{\eta}>0\)
- 当 \(\bar{\eta}_{p}\) 取不同的值,就得到了存在无风险证券时候的均值-方差前沿组合。\(\bar{\eta}_{p}=0,z_{p}=0\),即无风险资产。
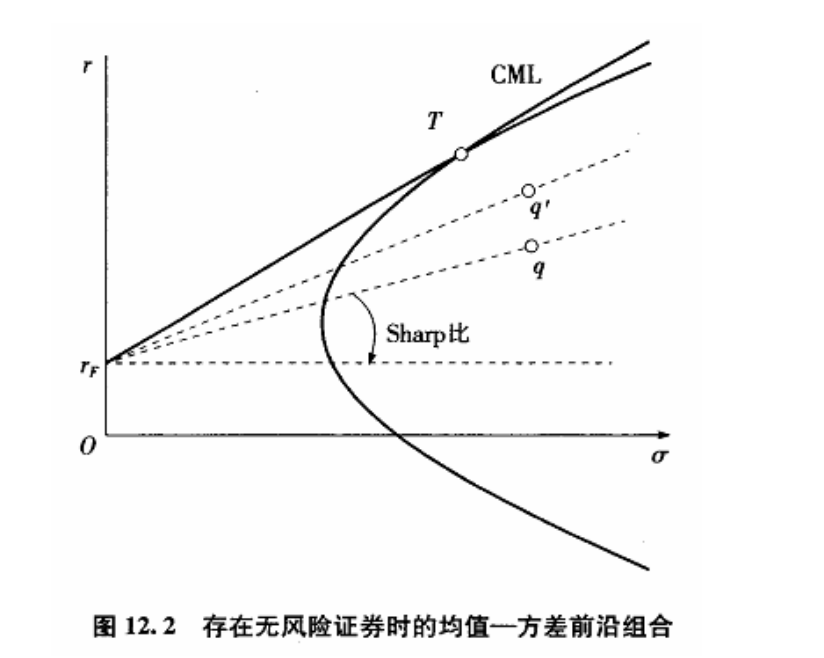
- 切点组合(只包含风险证券)
- \(\bar{\eta}_{r}=(\bar{\eta}^{T}\Sigma^{-1}\bar{\eta})/(\iota^{T}\Sigma^{-1}\bar{\eta})\), \(\iota^{T}z_{r}=1\)
- (构造出了一个超额收益率,其组合为为 1,只包含风险证券)
- \(z_{r}=\dfrac{1}{\iota^{T}\Sigma^{-1}\bar{\eta}}\Sigma^{-1}\bar{\eta}\)

- 任意 \(MVF\) 组合是 无风险证券 和切点组合 \(z_{r}\) 的线性组合
- Sharpe 比
-

- 即将所有风险债券看成一个组合
- 期望收益率 \(a\bar{r}_{q}\)
- 标准差 \(a\sigma_{q}\)
- where \(\bar{r}_{q},\sigma_{q}\) 分别为风险债券组合 \(q\) 的期望收益率和标准差
- \(\bar{r}-\sigma\) 平面上,这个组合在连接无风险债券和风险证券组合 \(q\) 的直线上(线性组合)
-
-

- 容易理解:只有 \(r_{F}\) 小于 \(r_{MVP}\) 的时候,其切线在 MVF 线的切点才可能在上半部分,也就是 MVE 组合。
- CML:capital market line, CML。所有选择来自 CML
- 夏普比率 Sharpe ratio
-
\(\text{Sharpe ratio}:=\dfrac{{\bar{r}_{q}-r_{F}}}{\sigma_{q}}\)
- 容易发现切点组合的 Sharpe ratio 最高。
- 这几何上就是斜率
-
\(\bar{r}_{q}-r_{F}=\beta_{q,p}(\bar{r}_{p}-r_{F}),\beta_{q,p}=Cov[\tilde{r}_{q},\tilde{r}_{p}]/Var[\tilde{r}_{p}]\)
- \(p\) 选为切点组合,则 \(\bar{r}_{q}-r_{F}=\beta_{q,T}(\bar{r}_{T}-r_{F})\)
- CAPM: capital asset pricing model
- 资本资产定价模型 CAPM
- \(\bar{r}_{n}-r_{F}=\beta_{n,M}(\bar{r}_{M}-r_{F})\)
- \(\beta=\frac{\mathrm{Cov}(R_a,R_m)}{\mathrm{Var}(R_m)}\)
- 定价简洁:风险溢价和市场风险(由对市场组合的 \(\beta\) 值定义)成正比
- 比例系数是 \(\bar{r}_{M}-r_{F}\),即市场组合的风险溢价
- 整个市场组合的 \(\beta\) 值为 1(自己和自己协方差等于方差,所以.). 它的风险溢价也叫做风险的价格(单位风险的风险溢价)

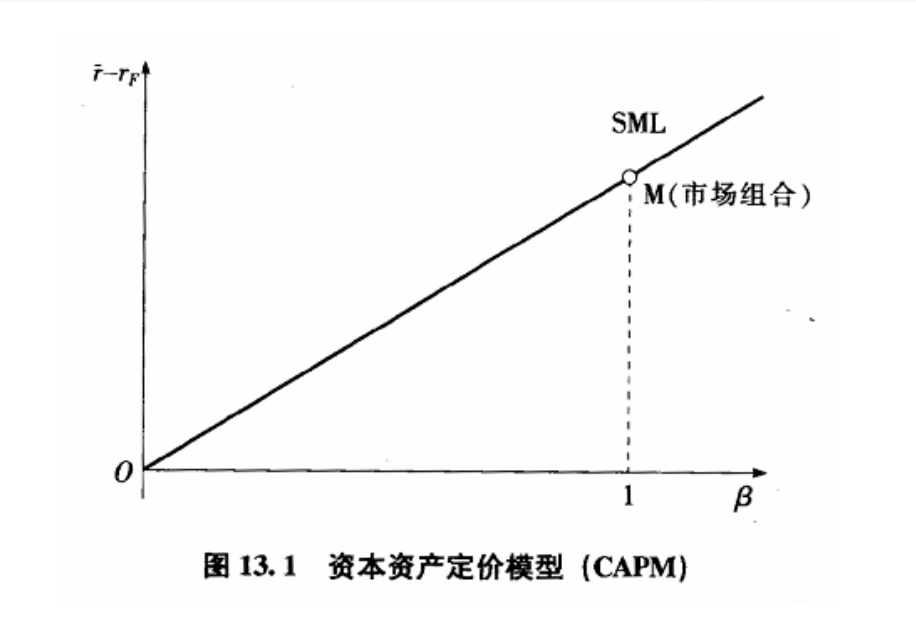
- 斜率为市场组合的风险溢价
- 把资产收益对市场收益做线性回归,可以得到
- 资本资产定价模型 CAPM
$$ \tilde{r}{n}-r{F}=\alpha_{n}+\beta_{n,M}(\tilde{r}{M}-r{F})+\tilde{\varepsilon}_{n} \tag{market regression} $$ - \(E[\tilde{\varepsilon}_{n}]=0,Cov[\tilde{r},\tilde{\varepsilon}_{n}]=0\),只是一个一般性的描述。 - 实际上这是一个单因子模型 - 均值方差框架,收益方差度量了资产的总风险。 - 所以我们对上面 market regression 两边取方差可以得到下面结论。 - \(\sigma^{2}_{n}=Var[\tilde{r}_{n}]\) - \(\sigma_{n,\varepsilon}=Var[\tilde{\varepsilon}_{n}]\) - 得到 -
$$
\sigma{2}{n}=\beta{n,M}{2}\sigma_{M}{2}+\sigma{2}_{n,\varepsilon}
$$
- 风险溢价不仅依赖于它负载的市场风险的大小,还取决于负载的方向即符号
- 例题 
- 上面讨论是存在无风险资产的情形,下面讨论不存在无风险资产的情形
- 定理
- 对于任意组合 \(q\)
$$ \bar{r}{q}-\bar{r}{zcm}=\beta_{q,M}(\bar{r}{M}-\bar{r}{zcm}) $$ \(zcm\) 是与市场组合协方差为 0 的 MVF 组合
- 实操定价

- 例题
假定你预测某上市公司一年后每股价值为100元,已知无风险利率为8%,市场期望收 益率为18%,公司β值为2.0,如果现在你想购买该公司的股票,你所愿意支付的合理价格应为多少?
- \(r_{a}-r_{F}=\beta_{a,M}(r_{M}-r_{F})=2.0\times(18\%-8\%)=20\%\)
- get \(r_{a}=20\%+r_{F}=28\%\)
- 根据定价原理
- \(p=\frac{\bar{q}(这里的payoff就是100元)}{1+28\%}=78.13元\)
-
这样才能保证到未来我不亏。(考虑风险的定价)
-
套利定价理论 APT
- 单因子模型
- Factor model
- 定义:假设证券的回报率只与不同的因子或者指标的运动有关的经济模型
- 因子模型 APT 的基础
- 单因子模型:证券的 回报率 生成过程只取决于唯一的因子
- 以这个唯一因子变化为自变量
- 形式
- \(r_{it}=a_{i}+b_{i}f_{t}+e_{it}\)
- \(f_t\):\(t\) 时期公共因子的预测值(唯一因素)
- 又称为因子风险(factor risk), 系统性的
- \(r_{it}\) :在时期 \(t\) 证券 \(i\) 的回报
- \(e_{it}\):在时期 \(t\) 证券 \(i\) 的特有回报
- 又称为 特殊风险 (idiosyncratic risk),剩余风险
- \(a_{i}\):零因子
- \(b_{i}\):证券 \(i\) 对公共因子 \(f\) 的敏感度(sensitivity)或因子载荷(factor loading)
- 为简单考虑,考虑特定时间的因子模型,省略 \(t\)
- \(r_{i}=a_{i}+b_{i}f+e_{i}\)
- 假设
- \(cov(e_{i},f)=0\)
- \(E[e_{i}]=0\)
- \(cov(e_{i},e_{j})=0\)
- 特有风险,没有风险系统性,也就是剩余风险的协方差矩阵是 对角矩阵
- 在这个模型下,讨论 均值和方差
- 均值:\(\bar{r}_{i}=a_{i}+b_{i}\bar{f}\)
- 方差: \(\sigma^{2}_{i}=b_{i}^{2}\sigma^{2}_{f}+\sigma_{ei}^{2}\)
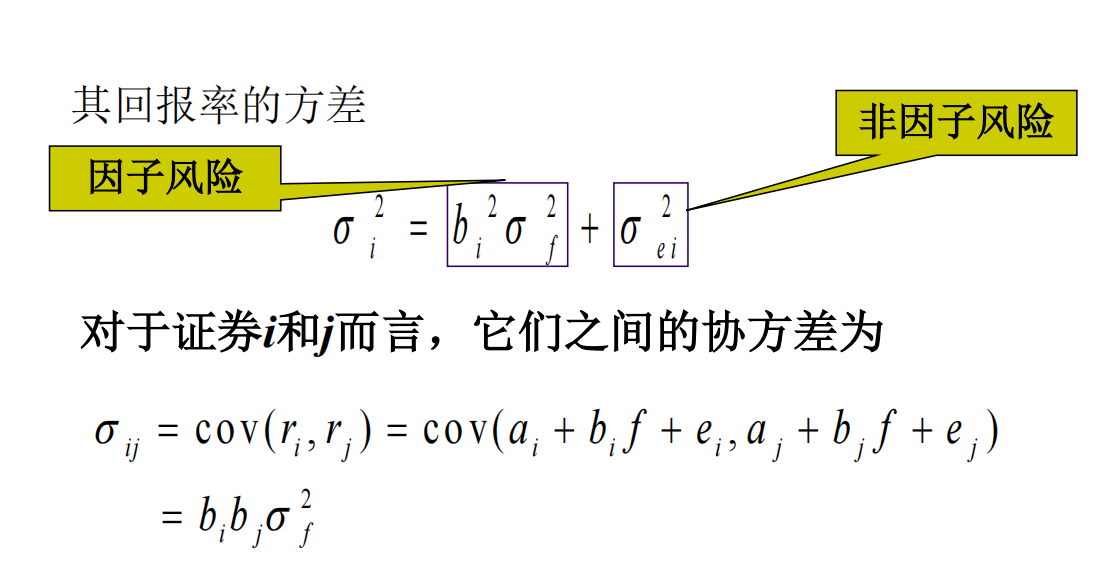
- 协方差:\(\sigma_{ij}=cov(r_{i},r_{j})=b_{i}b_{j}\sigma^{2}_{f}\)
- 优点:
- 简化估计量、计算量
- 风险的分散化
- 推论:CAPM模型为证券回报仅仅与市场因子回报有关的单因子模型
- 多因子模型
- \(r_{i}=a_{i}+b_{i_{1}}f_{1}+b_{i_{2}}f_{2}+e_{i}\)
- 套利机会
- 套利 (arbitrage) 定义:同时持有一种或者多种资产的多头或空头,从而不承担风险的情况下锁定一个高于无风险利率的收益
- free lunch
- 无套利原则
- 根据一价定律,两种具有相同风险的资产不能以不同的期望收益率出售
- 均衡的市场不会存在套利机会
- 套利活动会消除套利机会
- 套利 (arbitrage) 定义:同时持有一种或者多种资产的多头或空头,从而不承担风险的情况下锁定一个高于无风险利率的收益
- APT(套利定价)
- 基本原理:因子模型下,具有相同因子敏感性(sensitivity, \(b_{i}\))的资产应提供相同的期望收益率
- 假设
- 市场是有效的,完全竞争的,无摩擦的
- 投资者不知足。有套利机会就不断套利到无利可图
- 资产回报可以用如下的因子模型刻画
- 市场中证券种类远大于因子数目
$$ \tilde{r}{i}=E[\tilde{r}{i}]+b_{i_{1}}f_{1}+b_{i_{2}}f_{2}+\cdots+b_{im}f_{m}+e_{i} $$ - \(\tilde{r}_{i}\) 证券 \(i\) 的随机回报率 - \(b_{ij}\):证券 \(i\) 对第 \(j\) 个因子的敏感度 - \(f_{j}\):均值为零的第 \(j\) 个因子 - \(e_{i}\):证券 \(i\) 的随机项 - 构建套利组合 - 零投资 - 套利组合对一个证券的购买所需要的资金可以通过卖出别的证券来提供。自融资。(即换证券能带来收益,套利) - 无风险 - 因子模型中,因子波动导致风险。无风险即任何风险的敏感度都为 0 - 正收益 - 期望收益大于 0 假设套利证券组合是 \((w_{1},w_{2},\dots ,w_{i},\dots,w_{n})\) 数学上: $$ \begin{cases} \sum_{i=1}^{n}w_{i}=0 \ \sum_{i=1}^{n}b_{i}w_{i}=0 \ \sum_{i=1}^{n}w_{i}\bar{r}_{i}>0 \end{cases} $$ 方程组:依次表达:成本为 0,风险为 0,期望收益为正
- 套利的空间解释
- 拿三个证券举例子
- 无套利时,三种证券:
- \(\omega_{1}+\omega_{2}+\omega_{3}=0\)
- \(b_{1}\omega_{1}+b_{2}\omega_{2}+b_{3}\omega_{3}=0\)
- 故必然有 \(\bar{r}_{1}\omega_{1}+\bar{r}_{2}\omega_{2}+\bar{r}_{3}\omega_{3}=0\)
- 则可以理解为收益率向量 \(\mathbf{\bar{r}}\) 和组合向量 \(\boldsymbol{\omega}\) 正交
- 上面那个式子,如果用向量表达
$$
\begin{cases}
\sum_{i=1}{n}w_{i}=\mathbf{w}{T}\mathbf{1 }=0\
\mathbf{w}^{T}\mathbf{b}{1}=0 \
\mathbf{w}^{T}\mathbf{b}{2}=0 \
\dots \
\mathbf{w}^{T}\mathbf{b}{m}=0
\end{cases}
$$
- 不会套利均衡,即零投资无风险的组合必然无收益,则
$$
\sum{i=1}{n}w_{i}\bar{r}_{i}=\mathbf{w}{T}\bar{\mathbf{r}}=0
$$
等价于,只要
$$
\mathbf{w}\perp \mathbf{1},\mathbf{w}\perp \mathbf{b}_{j},j=1,\dots,m
$$
则对于任意的 \(\mathbf{w}\),必然有
$$
\mathbf{w}\perp \mathbf{\bar{r}}
$$
- 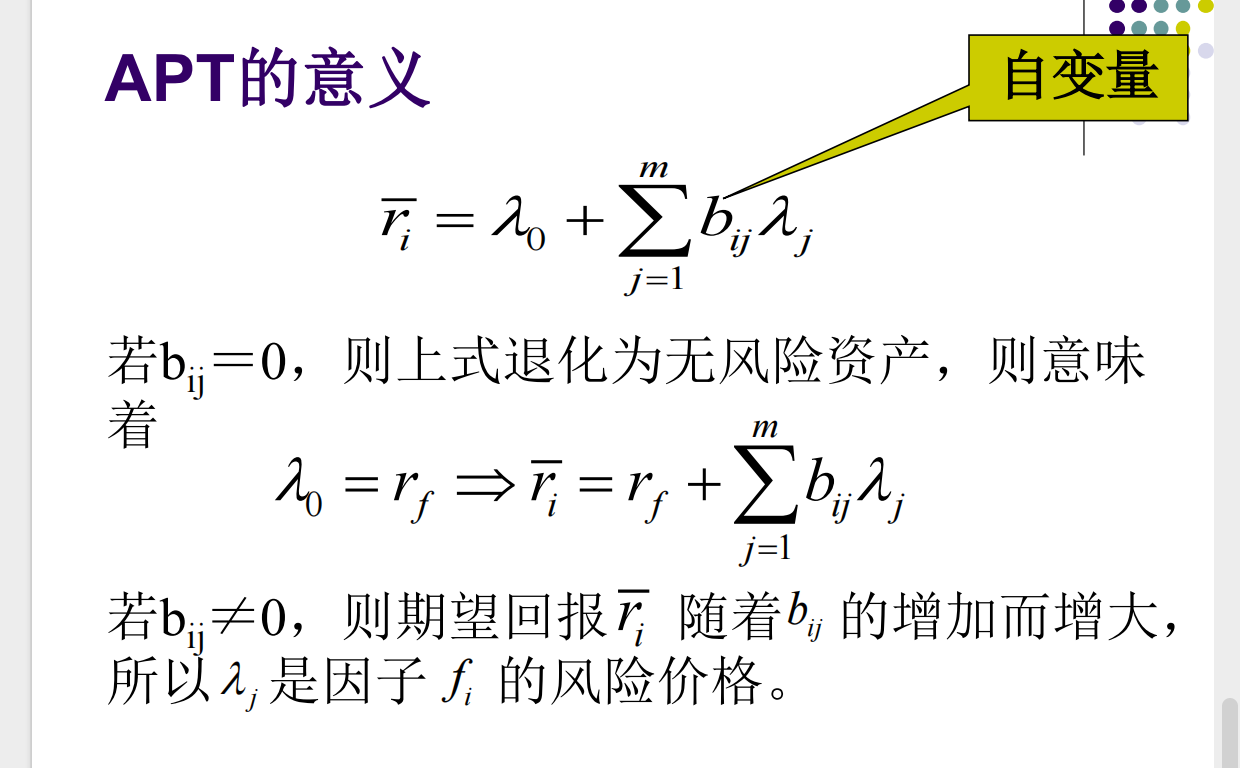 - 所以期望回报率向量 \(\mathbf{r}\) 一定可以表示为单位常向量和因子敏感度向量的线性组合
- 理解 APT
- \(\bar{r}_{i}=\lambda_{0}+\sum_{j}^{m}b_{ij}\lambda_{j}\)
- \(\lambda_{0}\) 是无风险收益率,\(\lambda _j\) 是因子 \(f_{i}\) 的风险价格
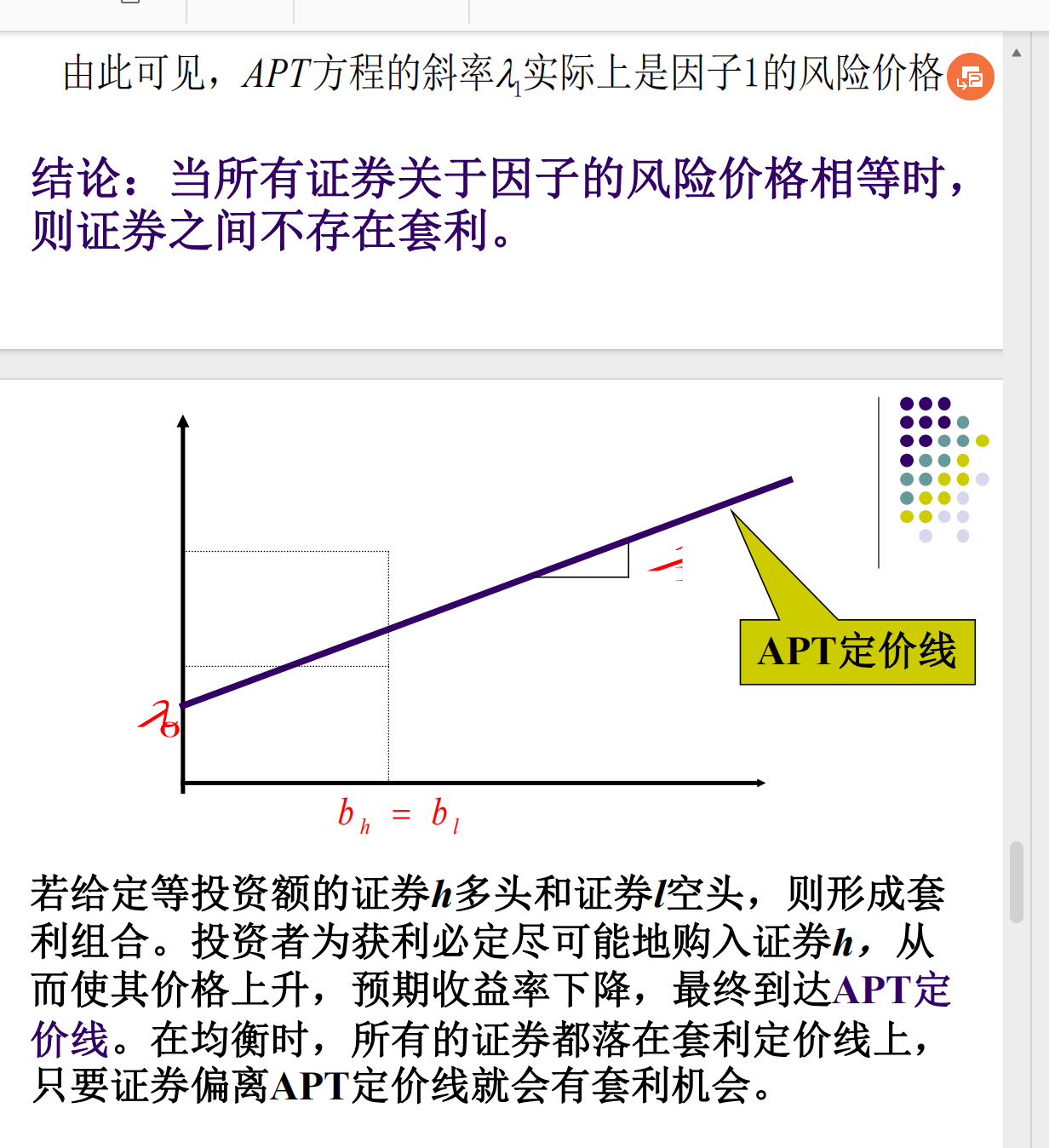
- APT 定价线
-
- 所以期望回报率向量 \(\mathbf{r}\) 一定可以表示为单位常向量和因子敏感度向量的线性组合
- 理解 APT
- \(\bar{r}_{i}=\lambda_{0}+\sum_{j}^{m}b_{ij}\lambda_{j}\)
- \(\lambda_{0}\) 是无风险收益率,\(\lambda _j\) 是因子 \(f_{i}\) 的风险价格
- APT 定价线
-