Section 2 ：数据的机器级表示与处理

——数值数据的表示
关于高级语言->机器语言

  • 表示
  • 链接
  • 执行

本章主要学习数据的机器级表示

Intro. Kahan 累加算法

  • 浮点数存在误差
    • 4000000 个 0.1(float) 相加（C 语言）结果可能不是 400,000
    • 为了解决累加误差，有经典的 Kahan 累加算法
1
2
3
4
5
6
7
8
9
10
11
function KahanSum(input)
    var sum = 0.0
    var c = 0.0          //A running compensation for lost low-order bits.
    for i = 1 to input.length do
        y = input[i] - c    //So far, so good: c is zero.
        t = sum + y         //Alas, sum is big, y small, so low-order digits of y are lost.
        c = (t - sum) - y   //(t - sum) recovers the high-order part of y; subtracting y recovers -(low part of y)
        sum = t             //Algebraically, c should always be zero. Beware eagerly optimising compilers!
        //Next time around, the lost low part will be added to y in a fresh attempt.
    return sum

  • 我们用一个独立的变量 c，记录被截断的低位。
  • 30000+3.14159=30003.1
  • 但是 30003.1-30000=3.1，可以与 sum 作差得到偏差。

数值数据的表示

  • 数值数据表示的三要素
    • 进位计数制
      • 十进制、二进制、十六进制、八进制？
    • 定/浮点表示（解决小数点问题）
      • 定点整数、定点小数
        • 定点整数默认小数点最右，定点小数默认小数点最左，都无需表示。
      • 浮点数
    • 编码
      • 原码 (Signed magnitude)
        • 缺点：0 的表示方法不唯一
          • 用首位表达正和负
          • 加减方法不唯一
          • 额外对符号化处理
      • 反码 (One’ s complement)
      • 补码 (Two’ s complement)
        • 使用模运算 (modular)
          • 时钟是一个模 12 系统，倒拨 4 和顺拨 8 是等价的
        • 结论 1
          • 一个负数的补码等于模减该负数的绝对值
          • 二进制系统推广
            • 一个负数的补码等于对应正数的“各位取反，末位+1”
            • 这实际是因为 k 位运算系统的模 2^k 可以表示为 2^k-1+1，而 2^(k-1)-x 等价于 x 的各位取反，最后再加上 1 即可
        • 结论 2
          • 对于某一确定的模，某数减去小于模的另一数，总可以用该数加上另一数负数的补码来代替。
        • 负数去哪里了？
          • 对于 short int 类型实现来思考，我们仍然可以用补码的思想，且保证首位是符号位
      • 移码 (Biased notation)
        • （浮点数的阶码）
        • 移码（biased exponent）是一种用来表示有符号整数的编码方式，主要用于浮点数表示中。它的核心思想是，在真值的基础上加上一个固定的偏移量（bias），从而将所有可能的负数和正数都映射成非负整数。
        • 移码没有符号位
1
2
3
4
5
6
7
8
9
10
#include<limits.h>
#include <stdio.h>
#include <stdint.h>
int main(){
	short a = INT8_MAX;
	short b = INT8_MIN;
	printf("%d,%d",a,b);
	return 0;
}
// out: 127, -128
  • 无符号数
    • unsigned int
  • 有符号数
    • int
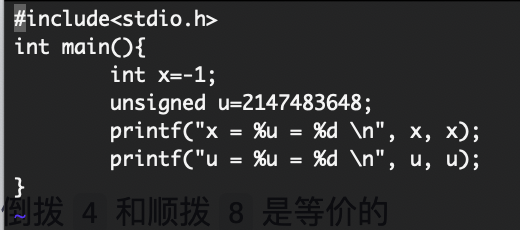
  • image.png|400
  • 这样一个程序在 C 90 运行结果如何？
    • note: 32bit system
  • image.png|400
  • 2147483648 实际上表示为二进制是 1 后面跟着 31 个 0

IEEE 754 表示法

IEEE 754 标准是目前最广泛使用的浮点数（Floating-Point Number）表示标准，被绝大多数现代处理器所采用。它定义了一种统一的方式来存储和处理非整数，极大地保证了不同计算机系统间浮点计算的一致性。

这个标准的核心思想是将一个浮点数拆分成三个部分：符号位、指数和尾数（或称有效数字）。

一个浮点数的最终值可以表示为：

$$
V=(-1)^{S}\times M\times 2^{E}
$$
其中：

  • S 是符号位（Sign）：占 1 个比特位，决定了数的正负。0 表示正数，1 表示负数。

  • M 是尾数（Mantissa/Significand）：表示数值的有效数字部分，通常用归一化形式表示，即小数点前有一个隐藏的 1。

    • 即除了二进制串的字符从 2^-1 开始算之外，你还需要一个隐藏的 1 加在尾数之前组成一个 1.xxx 的数

  • E 是指数（Exponent）：表示数值的量级大小，用偏移量（Bias）表示，以处理负指数。

单精度（Single-Precision，32 位）

  • 总共 32 位

  • 符号位：1 位 (第 31 位)

  • 指数：8 位 (第 23-30 位)

  • 尾数：23 位 (第 0-22 位)

指数的偏移量为 127。计算实际指数 $E_{real} = E_{stored} - 127$。

尾数采用归一化表示，默认隐藏了小数点前的 1。所以实际尾数 M_real = 1. M_stored。

双精度（Double-Precision，64 位）

  • 总共 64 位
  • 符号位：1 位 (第 63 位)
  • 指数：11 位 (第 52-62 位)
  • 尾数：52 位 (第 0-51 位)
    指数的偏移量为 1023。计算实际指数 E_real = E_stored - 1023。
    尾数同样采用归一化表示，默认隐藏了小数点前的 1。
    除了常规数值，IEEE 754 标准还定义了几个特殊值：
  • 正/负无穷大 (±∞)：指数部分全为 1，尾数部分全为 0。
  • 非数字（NaN，Not a Number）：指数部分全为 1，尾数部分非 0，表示无效或无法定义的计算结果（如 0/0）。
  • 非归一化数（Denormalized Number）：指数部分全为 0，尾数部分不为 0，用于表示非常接近于 0 的数。

have a try

-12.75

  • first, for -12.75 is a negative number, so sign bit is 1
  • second, for integer part, the binary representation of 12 is 1100
  • thirdly, consider 0.75, which is 0.5+0.25 = 2^(-1)+2^(-2), can be represented as 0.11_binary
  • Normalization
    • Use 科学计数法
    • 1100.11 = 1.10011 \times 2^3
    • now we have a pattern similar to standard form
    • M=10011
    • E=3, but IEEE have a offset of 127,
      • 3+127=130
      • convert 130 to an 8-bit binary number 10000010
  • Calculate Mantissa (尾数)
    • The normalized mantissa is 1.10011, The standard hides the leading 1, we only store the fractional part:
      • 10011
  • Combine the result
    Finally, we assemble the three parts in order: Sign bit | Exponent | Mantissa.
    • Sign: 1
    • Exponent: 10000010
    • Mantissa:
      • 10011000000000000000000

浮点数的非规格化表示 (Denormalized Representation)

在 IEEE 754 浮点数标准中，非规格化数（Denormalized Numbers 或 Subnormal Numbers）是一种特殊的表示形式，旨在填补最小正规格化数和零之间的“间隙”。

对于规格化数，我们知道其指数位不全为 0，并且尾数部分有一个隐藏的 1。这使得最小可表示数有一个较大的跳跃，直接从这个数跳到 0。为了解决这个问题，IEEE 754 标准引入了非规格化表示。

非规格化数的特点

  • 指数域全为 0：这是识别非规格化数最关键的特征。当指数部分的所有位都是 0 时，该浮点数被认为是非规格化的。

  • 尾数域不为 0：如果尾数域也为 0，则该数被定义为零。

  • 没有隐藏的 1：与规格化数不同，非规格化数的尾数部分没有隐藏的 1。其尾数的实际值就是其存储的值，即 0. M。

最小的非零正浮点数

非规格化数允许我们以更小的步长逐渐接近 0，从而提供更高的精度来表示非常小的数。

我们来计算一下**单精度（32 位）**浮点数中最小的非零正数。
根据非规格化数的定义：

  • 符号位：0（正数）
  • 指数域：00000000（全为 0）
  • 尾数域：最小非零值，即 00000000000000000000001（最后一位为 1，其余为 0）
    根据公式
    $$
    V=(-1)^{S}\times M\times 2^{E}
    $$
  • S = 0
  • 指数 E：在非规格化数中，实际指数值被定义为 1 - 偏移量，单精度的偏移量为127，所以 Ereal​=1−127=−126。
  • 尾数 M：由于没有隐藏的 1，其值为 0.00… 012​ （共 23 位），即 2−23。
    代入公式：

所以，单精度浮点数能表示的最小非零正数是 2^(-149)。

逻辑数据的编码表示

  • 表示
    • 用 1 bit 表示
    • True: 1
    • False: 0
  • 运算
    • 按位进行
  • 识别
    • 和数值数据形式上没有区别
    • When we use it, we use 指令 to indentify
  • 位串
    • 用来表示若干个状态位或控制位

西文字符的编码显示

  • 特点
    • 拼音文字，字符优先
    • 只对有限个字母、数学符号、标点符号等辅助字符编码
  • 表示
    • 常用：7 bit ASCII 码
    • 十进制数字 0-9
    • 英文字母: A-Z
    • 控制字符
  • 扩充 ASCII 字符集
    • ISO 8899
    • 这次是完整的 8 bit 空间了

汉字、国际字符的编码表示

  • 特点

    • 汉字是表意文字，一个字就是一个方块图形
    • 汉字数量巨大
      • 需要很大的码位

  • GB 2312

    • 2 bytes 表示一个汉字 16bit,65536
    • 一共收录 60000 多个简体字

  • CJK

    • 中日韩统一计划

  • GBK

    • 汉字内码拓展规范
    • 用首字节的 1 和 0 标记按双字节还是单字节解释，保证兼容性
      • 兼容 GB 2312

  • UCS

  • UTF-8 (UCS Transformation Form - 8)

    • 可变长形式
    • 可表示单字节-4 字节内容

  • UTF-16

    • 最常用。（固定用双字节表示字符）
    • 永远两个字节
    • 65536

汉字的字模点阵码和轮廓描述

汉字要表示，需要预先存储字体来渲染出来。

  • 点阵字体
    • 类似于一张图片，像素点画出汉字，形成点阵，存储点阵的位置。
    • 优点：可直接用输出设备如光栅显示，实现简单
    • 缺点：
      • 不方便加粗、斜体等格式修改，或者放大缩小会有失真。
    • image.png|400
  • 矢量字体
    • Postscript
    • TrueType Font
    • 更好的对字进行变化。

数据的基本宽度

  • bit 最小单位

  • 字节 (Byte)

    • 二进制信息的计量单位
    • 1 个字节=8 bit
    • 现代存储器通常按字节编地址
    • 此时，字节是最小可寻址单位
      • (addressable unit)

  • 字 word 也经常用来作为数据的长度单位

    • 1 个字一般是 16 bit

  • 字和 字长的概念不同

    • 字长：定点运算数据通路的宽度
      • CPU 内部的运算、存储、传送部件，宽度基本上一致才可以匹配。“字长”是内部的组织。
1
2
graph TD
A[高级语言程序]-->|编译汇编（必须了解硬件设计）|B[机器语言程序 机器数]

机器数（数据）的存储和排列顺序

  • 大端序
  • 小端序

如果以一个字节为排列单位，则

  • LSB(Least Significant Byte) 表示最低有效字节

  • MSB表示最高有效字节

  • ISA 设计的两个问题

    • 如何根据一个地址取到一个 32 位的字？
    • 一个字能否存放在任何地址边界？

大端方式和小端方式

Big Endian
Little Endian
大端（Big-Endian） 和 小端（Little-Endian） 是计算机存储数据时的两种不同字节顺序。它们主要影响多字节数据类型，比如整型（int）或浮点型（float）在内存中的存储方式。

可以把它们想象成书写多位数字（比如 1234）的两种不同方式：

  • 大端（Big-Endian）: 就像我们平时写数字一样，最高有效字节（MSB，Most Significant Byte）放在内存地址的最低位（最前面）。

    • 例如，数字 0x12345678 存储在内存中会是：12 34 56 78。

    • “大头在前”，这种方式更符合我们的阅读习惯。很多网络协议都采用大端序，所以它也被称为网络字节序。

  • 小端（Little-Endian）: 就像从右往左写数字一样，最低有效字节（LSB，Least Significant Byte）放在内存地址的最低位。

    • 例如，数字 0x12345678 存储在内存中会是：78 56 34 12。

    • “小头在前”，这种方式在大部分个人电脑（如基于 x 86 架构的处理器）和 ARM 处理器上比较常见。

简单对比
特性 大端（Big-Endian） 小端（Little-Endian）
存储顺序 高位字节存放在低位地址 低位字节存放在低位地址
形象比喻 正常阅读顺序，“大头在前” 反向阅读顺序，“小头在前”
常见场景 网络传输（网络字节序）、Java 虚拟机、PowerPC 个人电脑（Intel/AMD x 86 架构）、ARM 处理器
为什么需要了解它们？

在大多数情况下，作为开发者，你不需要关心字节序，因为编译器和操作系统已经处理好了。但是，当你进行跨平台通信或处理二进制文件时，字节序就变得至关重要。

例如，当一台大端机器向一台小端机器发送数据时，如果直接传输，接收方会因为字节顺序颠倒而错误地解析数据。这时就需要进行字节序转换，确保数据在不同系统间能正确地被理解。

在计网试验中你应该足够了解 [[vault/redkoldnote/docs/本科课程/计算机网络/exps/exp3/README|README]]

浮点数的加减运算

  • 对阶
    • 小阶往大阶对
    • 在进行加法之前，两个浮点数的阶码必须保持一致。因为浮点数是科学计数法的一种形式，比如 1.23×105 和 4.56×103，你不能直接把它们的有效数字（1.23 和 4.56）加起来。
    • 对阶的步骤是：
    • 比较两个浮点数的阶码，找出较大的那个。
    • 将阶码较小的那个数的小数部分向右移动，同时增加其阶码，直到两个数的阶码相等。
  • 对 IEEE 754 SP 格式来说，$\Delta E$ 大于多少时候，结果就等于阶大的那个数？（大数被小数吃掉）
    • 25
      • 符号位（Sign）：1 位
      • 阶码（Exponent）：8 位，采用移码表示
      • 小数部分/尾数（Fraction/Mantissa）：23 位
      • 由于有一个隐含头位 1，实际有效尾数为 24
  • Extra Bits （附加位）
    • IEEE 754 规定，后面跟着 2 bit 的 Extra Bits
    • guard digit, rounding digit
    • round digit: （就近舍入到偶数）
      • <1/2: then truncate （截去）
      • >1/2: then round up (add 1 to ULP)
      • =1/2: round up to nearest even bit
  • float 能精确刻画的十进制数位
    • image.png|400
    • 2^23=8388608, 7 bit
    • 表示范围不会溢出，但是精度会损耗
  • float 转化为 int 会精度损失，但是 double 就不会了.

Kahan sum 再看 [[#Intro. Kahan 累加算法]]

我们写一个 C 程序来看：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <stdio.h>

// Kahan 累加算法
float kahanSum(const float arr[], int n) {
    float sum = 0.0;
    float c = 0.0; // 补偿值
    
    for (int i = 0; i < n; i++) {
        float y = arr[i] - c; // 减去补偿值，得到需要累加的有效值
        float t = sum + y;    // 临时累加
        c = (t - sum) - y;     // 重新计算补偿值，捕获被舍弃的低位
        sum = t;               // 更新总和
    }
    
    return sum;
}

// 简单直接累加
float simpleSum(const float arr[], int n) {
    float sum = 0.0;
    for (int i = 0; i < n; i++) {
        sum += arr[i];
    }
    return sum;
}

int main() {
    // 构造一个数组，其中包含一个大数和一系列小数
    // 每次累加一个非常小的数
    const int N = 1000000;
    float arr[N];
    float small_number = 1.0e-8;
    
    for (int i = 0; i < N; i++) {
        arr[i] = small_number;
    }
    
    printf("数组中包含 %d 个 %.10f\n", n, small_number);
    printf("理论上的精确值是：%.10f\n", n * small_number);
    printf("-----------------------------------\n");

    // 直接累加
    float result_simple = simplesum(arr, n);
    printf("简单累加的结果: %.10f\n", result_simple);

    // kahan 累加
    float result_kahan = kahansum(arr, n);
    printf("kahan累加的结果: %.10f\n", result_kahan);

    // 比较结果
    printf("-----------------------------------\n");
    printf("结果差异（简单累加 - kahan累加）: %.10f\n", result_simple - result_kahan);
    
    return 0;
}
  • output
  • image.png|400